| Linear inequalities are also called first
degree inequalities, as the highest power of the variable (or pronumeral)
in these inequalities is 1.
E.g. 4x > 20 is an inequality of the first degree,
which is often called a linear inequality.
Many problems can be solved using linear inequalities.
We know that a linear equation with one pronumeral has only one value
for the solution that holds true. For example, the linear equation 6x = 24 is a true statement only when x = 4. However, the
linear inequality 6x > 24 is satisfied when x > 4. So,
there are many values of x which will satisfy the inequality 6x
> 24.

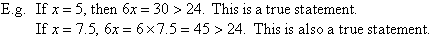
Similarly, we can show that all numbers greater than 4 satisfy this
inequality.
Inequalities Involving One Operation
Recall that:
- the same number can be subtracted from both sides of an inequality
- the same number can be added to both sides of an inequality
- both sides of an inequality can be multiplied (or divided) by the
same positive number
- if an inequality is multiplied (or divided) by the same negative
number, then:
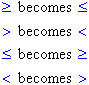
Subtracting a Number from Each Side of an Inequality
Subtracting a number from each side of an inequality does not change
the sign of the inequality.
Example 21
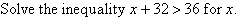
Solution:

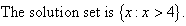
Note:
(i) The solution set consists of all numbers greater than 4, and
is shown on the number line as follows:

The ring at 4 in this diagram means that 4 is not an element of the
solution set.
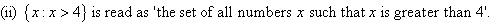
Example 22
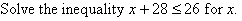
Solution:
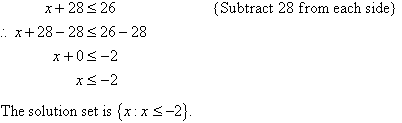
Note:
(i) The solution set consists of all numbers less than or equal
to –2,
as shown on the following number line.
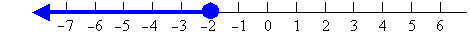
The solid dot at –2
in the diagram means that –2 is an element of the solution set.
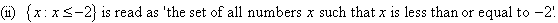
Key Terms
linear inequalities, first
degree inequalities |