In general:

The odds against winning are found by calculating:
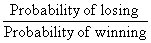

Let A be the event of winning (i.e. A' is the
event of losing).
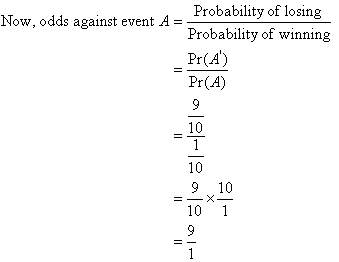
The odds against winning (i.e. the odds the horse will lose) are
9:1. We usually say the 'odds on' to win are 9:1.
Bookmakers assign odds against winning events in sport, horse racing,
greyhound racing etc. So, if a bookmaker assigns odds of 9:1 without
allowing for a profit margin, then a competitor is given 9 chances of
losing and one chance of winning out of 10 chances. That is:
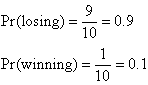
Note that if a gambler places a $1 bet with a bookmaker at 9:1 odds on
to win and his horse wins, the gambler will win $9 plus the $1 bet,
obtaining $10; otherwise the gambler will lose $1. If a $5 bet is placed
with the bookmaker at 9:1 and his horse wins, the gambler will win $45
plus the $5 bet, obtaining $50; otherwise the gambler will lose $5.
Past performance, the recent form of competitors, the expected weather
conditions for the event, the jockey and other relevant factors are taken
into consideration to determine the odds before the occurrence of the
event. As gamblers place their bets, bookmakers adjust the odds in order
to minimise the amounts paid out and thus maximise their profit, i.e. the
bookmakers alter the odds so that they make a profit. The bookmakers' odds
are decided on subjective estimates of probabilities biased in their
favour.
Example 8
What are the odds in favour of throwing a 1 with a die?
Solution:
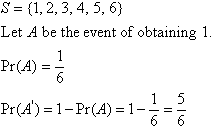
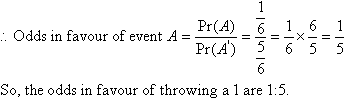
Example 9
If there is a 30% chance of winning, find the odds against winning.
Solution:
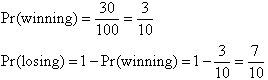
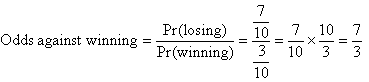
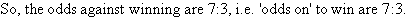
Example 10
If the odds against winning a horse race are 2:1, find the probability
of winning the race.
Solution:
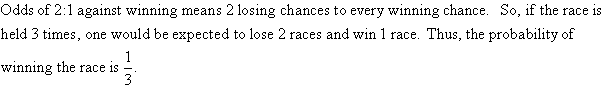
Example 11
If the odds in favour of winning a race are 3:5, find the probability
of winning the race.
Solution:
Odds in favour of winning a race of 3:5 mean 3 chances of winning to
every 5 chances of losing. So, if the race were held 8 times, one would be
expected to win 3 races and lose 5 races. 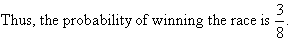
Example 12
I bet $4 on a horse race. How much would I receive from the bookmaker
if a win results with the following odds on to win?
a. evens
b. 3:1
c. 5:2
Solution:
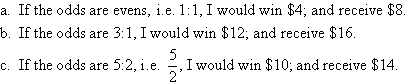
Example 13
If there is a 0% chance of winning, can we find the odds against
winning?
Solution:

So, we cannot find the odds against winning.
Key Terms
odds, odds against winning, odds on to win |