Year 10 Interactive Maths - Second Edition

Projects

Flags (or motifs) can represent national symbols, beliefs and bind people of the same nationality or affiliation.

Project 6.1  Motifs

Five-pointed star

• Draw a circle of radius 6 cm.
• Mark a point at the top of the circle; and divide the 360º at the centre of the circle into five equal angles. Mark off the other four points of the star.
• Number the points 1 to 5 and join 1 to 3, 3 to 5, 5 to 2, 2 to 4 and 4 to 1 as shown.
• Draw solid lines over the outline of the star.
• Erase the construction lines (i.e. the dotted lines).
• Colour the star.

The president suggested that the 12-pointed star is to be inscribed in a circle of radius 6 cm; and constructed by following instructions similar to the instructions for constructing a 5-pointed star. Number the points 1 to 12 as for a clock face and join 12 to 2, 2 to 4 and so on (joining n to n + 2). If the 12-pointed star is not obtained, join 12 to 3, 3 to 6 and so on (joining n to n + 3). If the 12-pointed star is still not obtained, try all other possibilities until you have succeeded in constructing one; and shade the star with the colour red (or blue).

Your report should include the following:

1.  Statement of the problem
2.  Method used to solve the problem
3.  All working and diagrams
4.  Conclusion
5.  Acknowledgments

Project 6.2  The Flag

The symbol used on the flag of South Korea represents the balance of opposing forces in the world such as slow and fast, bright and dim, active and idle, hot and cold etc.

• Draw a circle of radius 6 cm.
• Divide the horizontal diameter into four equal parts.
• Draw two semi-circles centred at A and B which meet at the centre O and end at C and D respectively.
• Draw solid lines over the circle and the semi-circles.
• Erase the construction lines.
• Shade the two regions of the symbol with the colours red and blue respectively.

The flag bears a red and blue symbol, similar to the flag of South Korea, on a white background. All material is available in rolls 10 m long by 1 m wide.

1.  State the minimum length of material required for each colour.
2.  Determine the wastage of material (in square metres) for each colour. Hence find the percentage
     wastage of material for each colour.
3.  Your manager suggests an increase in the size of the symbol, as shown in the diagram.

a.  How much material is wasted for each colour?
b.  What is the percentage wastage of material for each colour?
c.  What is the area of the largest circular symbol that could be made?

Your report should include the following:

1.  Statement of the problem
2.  Method used to solve the problem
3.  All working and diagrams
4.  Conclusion
5.  Acknowledgments

Project 6.3  The Golden Ratio

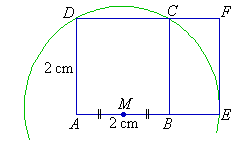
Draw a square ABCD of side 2 cm. With M, the midpoint of AB, as a centre and radius MD, draw an arc to meet AB extended at E. Construct the rectangle AEFD; and then erase the construction lines.

The rectangle thus obtained is called a golden rectangle; and is often used in buildings and paintings.

1.  Use Pythagoras' Theorem to find:

a.  MC
b. MD

2.  Find the length of the following line segments:

a.  ME
b.  AE
c.  MF
d.  AF

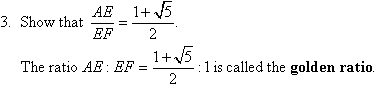
4.  Use a calculator to find the golden ratio correct to 4 decimal places.

Extension

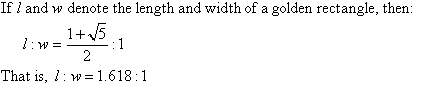
The number 1.618 is called the golden number.

5.

a.  Draw a rectangle ABCD with AB = 89 mm and BC = 55 mm.
b.  Is ABCD a golden rectangle?  Justify your answer.
c.  Construct a series of squares as shown in the following diagram; and verify that each remaining rectangle is a golden one.

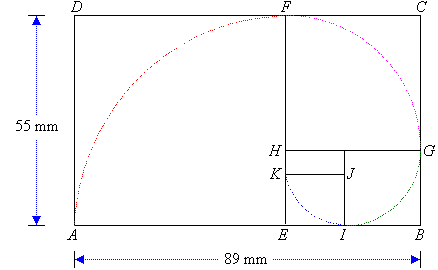
Golden Spiral

6.  With centre E and radius EA draw an arc from A to F. With centre H and radius HF draw an arc from F to G; and continue this process as far as possible.

The spiral thus obtained is called the golden spiral and occurs often in nature.

Your report should include all of your working and diagrams.

Project 6.4  Spirals

If a point moves continually clockwise (or anticlockwise) about and at an increasing distance from a central point, then the path traced out is said to be a spiral.

Archimedes, the Greek mathematician, discovered the spiral known as the Spiral of Archimedes.

1.

a.  Draw a series of 12 radiating lines 30º apart.
b.  Make a point 3 mm from the centre on one of the lines.
c.  Move in an anticlockwise direction to the next radiating line and mark a point 6 mm from the centre.
d.  Keep moving to successive lines and increasing the distance from the central point by 3 mm each time.
e. Join the points by a smooth curve; and erase the construction (i.e. dotted) lines.

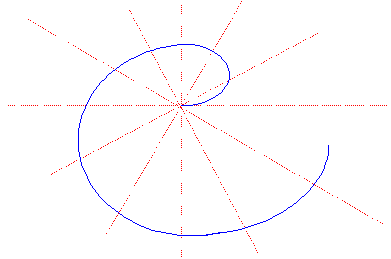
The curve thus obtained is the Spiral of Archimedes.

Extension

2.

a.  Draw a Spiral of Archimedes which has radiating lines 10º apart by moving only 2 mm more from the centre along the next radiating line in an anticlockwise direction.
b.  How do the characteristics of the second spiral differ from the characteristics of the first spiral drawn?

René Descartes, the French mathematician, discovered the equiangular spiral which approximates the spiral in nautilus shells and other shells of cephalopods.

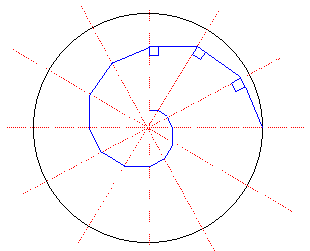
3.

a.  Draw a dotted circle of radius 2.2 cm.
b.  Draw a series of 12 radiating lines 30º apart.
c.  Select a point on the circle where it meets a radius; and drop a perpendicular line from the next radius in an anticlockwise direction to this point.
d.  From a point on the third radius, drop a perpendicular line to meet the first perpendicular line drawn.
e.  Continue this process as long as you can (i.e. until you reach the central point).
f.  Erase the construction lines. The curve thus obtained is an equiangular spiral.
g.  Where does the equiangular spiral terminate?

4.

a.  Draw an equiangular spiral, which has radiating lines 20º apart.
b.  How do the features of the second spiral differ from the features of the first spiral drawn?

5.  Compare the characteristics of the Spiral of Archimedes and the equiangular spiral.

Your report should include all of your working and diagrams.