Project 9.1 Modelling Surds

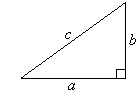
Draw a horizontal line OX, and construct a right-angled triangle OAB so that OA = AB = 1 cm.
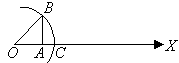
1. Find:
a. the exact distance OB
b. the approximate distance OB correct to 1 decimal place
With O as centre and radius OB, draw an arc to meet OX at C.
2. Which real number is modelled by point C?
3. Can you geometrically model the following real numbers?
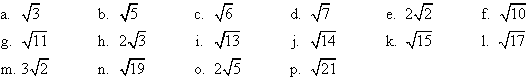
Use a ruler and/or calculator to verify your answer.
4. Use Microsoft® Excel to verify your answers for question 3.
Your report should include all working and diagrams.
Project 9.2 Rational Approximation of a Square Root
Formulas containing square roots often occur in science. To perform
numerical computations, we need to find a rational number that
approximates the value of the square roots.
The square roots of numbers have been computed and printed in
mathematical tables. But you may wonder how the tables were computed. The
answer is by intelligent guesswork and an iterative method.
Intelligent Guesswork
Consider the square root of 7.

Natural numbers are evenly placed on the number line; and we notice
that the perfect squares on either side of 7 are 4 and 9. Therefore, the
square root of 7 lies between 2 and 3, as shown in the diagram.
There are 5 units between 4 and 9; and 7 is 3 units above 4.
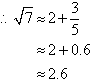
Iterative Method
We adopt the following steps to find the square root of a number, N.

Continue this process until you obtain the required degree of accuracy.
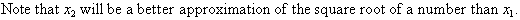
Let us compute the square root of 7 to illustrate the iterative process.

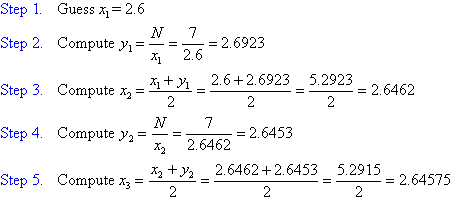

Use a calculator to verify this answer.
1. Tabulate the square roots of natural numbers between 1 and 100
using a graphical method and/or intelligent guesswork.
2. Use a graphical method and/or intelligent guesswork to
compute:
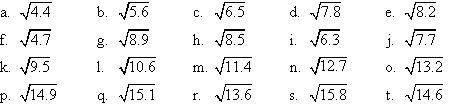
3. Tabulate the square roots (correct to 3 decimal places) of natural
numbers between 1 and 100 using the iterative method.
4. Tabulate the square roots (correct to 3 decimal places) of
natural numbers between 1 and 100 using Microsoft ® Excel.
5. Compare the computational performance of the different
methods.
Project 9.3 Perfect Numbers
If the sum of all factors of a number is twice the number, then it is
said to be a perfect number.
For example, 6 is a perfect number as illustrated below.
6 = 1 × 6 = 2 × 3
So, the factors of 6 are 1, 2, 3 and 6.

Hence 6 is a perfect number.
1a. By trial and error, find the next perfect number.
b. The next perfect number is between 490 and 500. By trial
and error, find this perfect number.
2a. Factors of 6 are 1, 2, 3 and 6. Find the sum of the reciprocals
of the factors of the perfect number 6.
b. Investigate the sum of the reciprocals of factors of the
perfect number found in 1(b).
3. The perfect number 6 can be expressed as a sum of powers of 2.
That is:
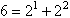
Investigate whether every perfect number is a sum of powers of 2. |