Project 3.1 The Sieve of Eratosthenes
A Greek mathematician, Eratosthenes (276-195 BC), discovered the Sieve
which is known as the Sieve of Eratosthenes. He migrated to Egypt; and
taught at the University of Alexandria.
1. Copy the following table of whole numbers and cross out the
number 1, as shown below.

2. Circle the number 2 and then cross out all the multiples of 2,
as shown below.
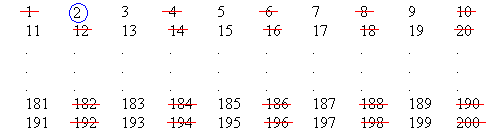
3. The next number that is not crossed out is 3. Circle it
and then cross out all the multiples of 3 (i.e. 3, 6, 9, 12...).
4. The next number that is not crossed out is 5. Circle it
and then cross out all the multiples of 5 (i.e. 5, 10, 15, 20…).
5. The next number that is not crossed out is 7. Circle it
and then cross out all the multiples of 7.
6. Continue this process until there is no 'next number'.
7. Make a list of all the circled numbers.
8. Write the factors of each of the circled numbers.
9. Make a list of the first twenty crossed out numbers and write
the factors of these numbers.
10. What do you observe about the number of factors of the circled
numbers and the crossed out numbers? Write a brief statement in your
own words.
11. What name is given to the circled numbers?
12. What name is given to the crossed out numbers?
13. How many prime numbers are less than 100?
14. How many prime numbers are less than 200?
15. Twin primes are two primes that differ by 2.
E.g. 3 and 5 are twin primes because they differ by 2. Clearly,
7 and 11 are not twin primes because they differ by 4.
Use the Sieve of Eratosthenes to find other twin primes between 2 and
200.
16. If the digits of a prime number are reversed, then the numbers
thus obtained is sometimes a prime. E.g. 17 and 71 are both
primes. However, 23 and 32 are not primes.
From your list of prime numbers (or the Sieve of Eratosthenes), find
other pairs like 17 and 71.
|