| Angles are used in daily life. Engineers and architects use angles for
designs, roads, buildings and sporting facilities. Athletes use angles to
enhance their performance. Carpenters use angles to make chairs, tables and
sofas. Artists use their knowledge of angles to sketch portraits and
paintings.
If two lines meet (or intersect) at a point, then an angle is formed.
The point of intersection of the lines is called the vertex.
An angle is shown below.
Lines AB and AC meet at the point A to form an
angle. The point A is the vertex of the angle, and the lines that
meet to make the angle are called the arms of the angle.
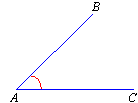
Naming Angles
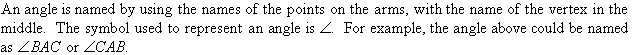
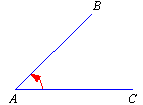
Size of an Angle
The amount of turn from one arm of the angle to the other is said to be
the size of an angle.
The size of an angle is measured in degrees; and the symbol used
to represent degree is º. There are 360º in a full turn (or circle).
Note:
A degree is defined such that the angle of one full turn (or
circle) is 360 degrees.
Measuring Angles
A protractor is used to measure angles. In this section, we will
consider the use of a protractor that has the shape of a semi-circle and two
scales marked from 0º to 180º.
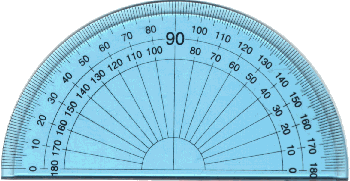
The two scales make it easy for us to measure
angles facing different ways.
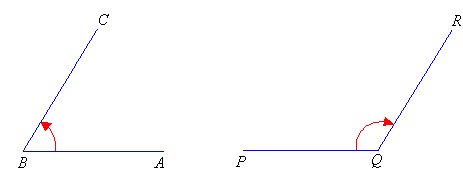
To measure the size of angle ABC, place the protractor over the
angle so that the centre of the protractor is directly over the angle's
vertex, B; and the base line of the protractor is along the arm, BA,
of the angle.
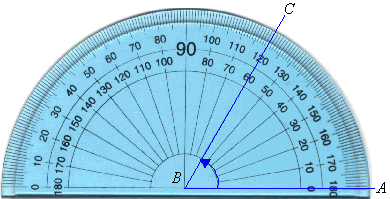
We use the inner scale to measure the angle ABC, as the arm AB passes through the zero of the inner scale. Following
the inner scale around the protractor, we find that the other arm, BC,
passes through the inner scale at 60º. So, the size of angle ABC is
60 degrees. We write this as follows:
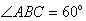
To measure the size of angle PQR, place the protractor over the
angle so that the centre of the protractor is directly over the angle's
vertex, Q; and the base line of the protractor is along the arm, PQ,
of the angle.
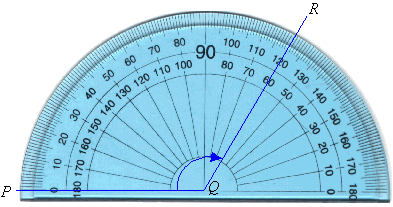
We use the outer scale to measure the angle PQR, as the arm PQ passes through the zero of the outer scale. Following
the outer scale around the protractor, we find that the other arm, QR,
passes through the outer scale at 120º. So, the size of angle PQR is
120 degrees. We write this as follows:
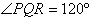
Types of Angles
Angles are classified according to their size.
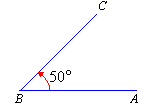
An acute angle is greater than 0º and less than 90º.
A right angle equals exactly 90º.
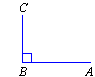
Note that a right angle is marked on the diagram as a small square.
An obtuse angle is greater than 90º and less than 180º.
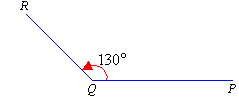
A straight angle equals exactly 180º.

A reflex angle is greater than 180º and less than 360º.
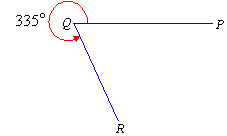
A perigon (or a revolution) is an angle that equals exactly
360º.
Measuring Reflex Angles
Recall that:
A protractor can be used to measure the size of an acute angle (between
0º and 90º) and an obtuse angle (between 90º and 180º).
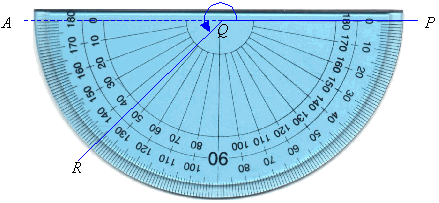
Now, we will use a protractor to measure the reflex angle PQR.
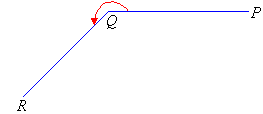
To measure the reflex angle PQR, extend the arm PQ to A to form angle PQA which is a straight angle. Then measure the size of
the angle AQR and add 180º.
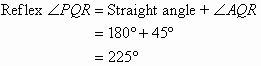
Key Terms
point, angle, vertex, arms of the angle, size of an angle, degrees, protractor, inner
scale, outer scale, acute angle, right angle, obtuse angle, straight
angle, reflex angle, perigon, revolution |