Tables and graphs are useful to find a pattern between the y-coordinate and the x-coordinate.
Using Tables
We can find a pattern in coordinates by listing their ordered pairs in a
table.
Example 7
Consider the following table.
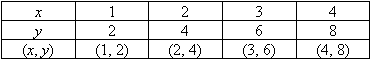
a. Describe the relationship between the y-coordinate and
the x-coordinate in words.
b. Find the algebraic relationship between x and y.
Solution:
a. By trial and error, we look for a relationship between the
values of x and y.
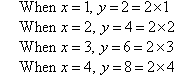
We can describe the relationship between x and y in words as follows:
The y-coordinate is twice the x-coordinate
This means y is twice x.
b. So, the algebraic relationship between the x-coordinate
and y-coordinate is:
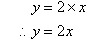
Using Graphs
We can find a pattern in coordinates by drawing a graph of their ordered pairs.
Example 8
a. Plot the following points on a Cartesian plane:
A(1, 3), B(2, 6), C(3, 9), D(4, 12), E(5,
15), F(6, 18)
Use a ruler to join the points A, B, C, D, E and F.
b. Describe the relationship between the y-coordinate
and the x-coordinate in words.
c. Find the algebraic relationship between x and y.
Solution:
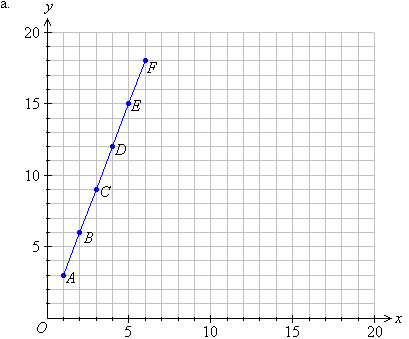
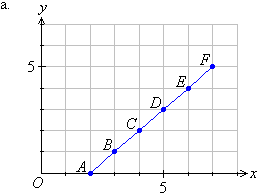
b. We notice that the points lie on a line. Such a pattern is
called a linear relationship because it represents a straight line
relationship between the coordinates of the points.
We can describe the relationship between x and y in words
as follows: The y-coordinate is three times the x-coordinate.
This means y is three times x.
c. So, the algebraic relationship between the x-coordinate
and y-coordinate is:
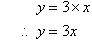
Example 9
a. Plot the following points on a Cartesian plane:
A(2, 0), B(3, 1), C(4, 2), D(5, 3), E(6,
4) and F(7, 5)
Use a ruler to join the points A, B, C, D, E and F.
b. Describe the relationship between the y-coordinate and the x-coordinate
in words.
c. Find the algebraic relationship between x and y.
Solution:
b. We notice that the points lie on a line. Such a pattern is called a linear
relationship because it represents a straight line relationship between
the coordinates of the points in the pattern.
We can describe the relationship between x and y in words
as follows:
The y-coordinate is two less than the x-coordinate
c. So algebraically, the relationship between the x-coordinate and y-coordinate is:
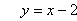
Using a Difference Pattern
When we look for a pattern in ordered pairs, we can find the difference
between two successive values of y. This allows us to find a rule as
illustrated below.
Consider the following table.
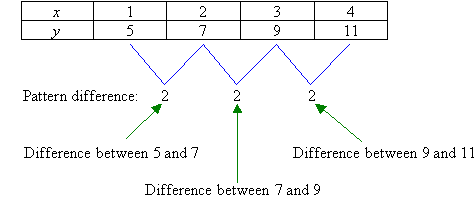
We notice that the values of x increase by just one at a time and
the difference between the successive values of y is 2. So, the rule
starts off with y = 2x. Will this give a correct answer from
the table? Let us check.
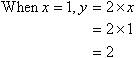
The answer is no. From the table, when x = 1 the
value of y should be 5. How do we change our answer from 2 to 5?
We
should add 3.
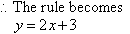
Check the rule to see if it is correct:
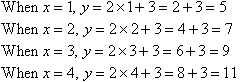
Key Terms
tables, graphs, linear
relationships, difference pattern |