Prime factors are used to find the highest common factor (HCF) and the lowest common multiple (LCM) of two (or more) large numbers.
Highest Common Factor (HCF) by Prime Factors
The HCF of two (or more) numbers is the product of common prime factors.
Example 22
Find the HCF of 300 and 375.
Solution:
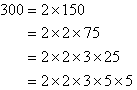
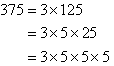
Organise the above information as shown below and circle the prime factors that are common to both numbers. The HCF is the product of
common prime factors.
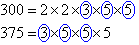
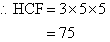
Note:
- 300 = 4 × 75 and 375 = 5 × 75.
- 75 is the largest factor common to 300 and 375.
Lowest Common Multiple (LCM) by Prime Factors
The LCM of two (or more) numbers is calculated as follows:
- Express the numbers as a product of prime factors.
- Circle all of the prime factors of the smaller of the two numbers.
- Circle any prime factors of a larger number that have not already been
circled for the smaller number (or smaller numbers if you are looking
for the LCM of more than two numbers).
- The LCM is the product of the circled prime factors.
These steps are better understood by reading the following examples.
Example 23
Find the LCM of 300 and 375.
Solution:
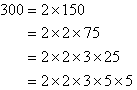
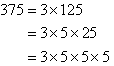
Organise the above information as shown below and circle all of the prime
factors of the smaller number. Then circle any prime factors of the
larger number that have not already been circled in the smaller
number. The LCM is the product of the circled prime factors.

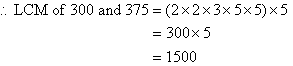
Note:
- The product of prime factors of 375 has three 5s but the product of
prime factors of 300 has only two 5s. Since we circled two 5s for
300, we must circle the extra 5 for 375 as shown above.
- 1500 is a multiple of 300 as 5 × 300 = 1500.
- 1500 is a multiple of 375 as 4 × 375 = 1500.
Example 24
Find the LCM of 6 and 8.
Solution:
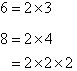
Organise the above information and circle all of the prime factors of the
smaller number as shown below. Then circle any prime factors of the
larger number that have not already been circled in the smaller
number. The LCM is the product of circled prime factors.
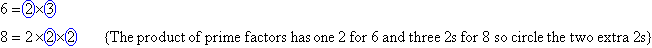
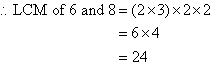
Finding a Pattern
By observation from Example 24, we find that:
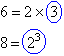

In general:
The lowest common multiple of two (or more) numbers can be
computed as follows:
- Express each number as a product of its prime factors using powers.
- Then circle the prime factors to the highest power from the given
numbers.
- Find the product of each prime factor to its highest power from the
given numbers. This product represents the LCM of the numbers.
Example 25
Find the LCM of 9, 40 and 48.
Solution:
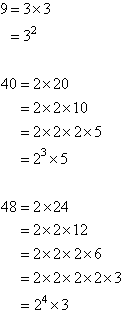
Organise the above information and circle each prime factor with its
highest power as shown below. The highest power of 2 is 24, the
highest power of 3 is 32 and the highest power of 5 is 51.
So, circle 24, 32 and 51. The LCM is the
product of the prime factors to the highest powers.
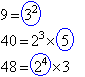

|