Bisect means to cut in half. In this section, we will consider
the methods to bisect an angle and a line segment.
Bisector of an Angle
The steps required to bisect (cut in half) an angle are shown in the
following example.
Example 3
Use a ruler and compass to bisect the angle ABC:
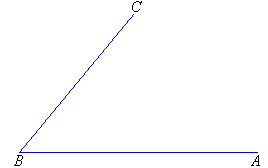
Solution:
Step 1: Draw an arc with B as the centre to cut the
arms, BA and BC, of the angle at P and Q respectively.
Step 2: Using the same radius, draw an arc centred at P.
Step 3: With centre Q and using the same radius, draw an
arc to cut the arc in Step 2 at R.
Step 4: Join, B, the vertex of the angle to the point R.
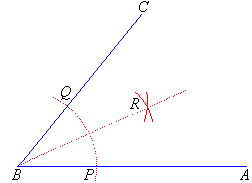
BR bisects the angle ABC, and is called the bisector of
angle ABC.
Perpendicular Bisector of a Line Segment
The steps required to construct a perpendicular bisector of a line
segment are shown in the following example.
Example 4
Use a ruler and compass to perpendicularly bisect a line, AB, 8 cm
long.
Solution:
Step 1: Draw a line, AB, 8 cm long.
Step 2: Draw an arc centred at A with a radius of more
than half of the length of AB.
Step 3: Using the same radius, draw an arc centred at B to cut the arc drawn in Step 2 at P and Q.
Step 4: Join PQ.
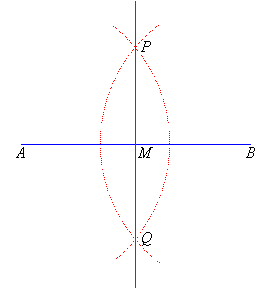
PQ perpendicularly bisects AB at M; and PQ is
called the perpendicular bisector of the line segment AB.
Perpendicular from a Point onto a Line
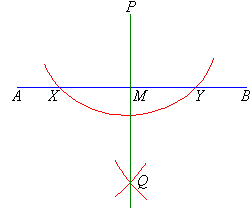
Example 5
Draw a line, AB, 7 cm long. Then use a compass to drop a
perpendicular from a point, P, which is approximately 6 cm from the
line.
Solution:
Step 1: Draw a line, AB, 7 cm long.
Step 2: Draw an arc centred at P with a radius that is
long enough to cut the line AB at two points, X and Y.
Step 3: Draw an arc centred at X using a radius that is
more than half of the length of the interval XY. You could use the
radius PX.
Step 4: Using the same radius, draw an arc centred at Y to cut the arc drawn in Step 3 at Q.
Step 5: Join PQ.
Note:
Perpendicular at a Point on a Line
Example 6
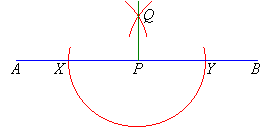
Draw a line, AB. Then use a compass to construct a
perpendicular to the line AB at a point, P, on the line.
Solution:
Step 1: Draw a line, AB, and mark the point P on the line.
Step 2: Draw an arc centred at P that cuts the line AB at two points, X and Y.
Step 3: Draw an arc centred at X; using a radius that is
longer than half of the length of XY.
Step 4: Using the same radius, draw an arc centred at Y to cut the arc drawn in Step 3 at Q.
Step 5: Join PQ.
Activity 10.2

Key Terms
bisect, bisector of an angle, perpendicular
bisector of a line segment, perpendicular from a point onto a
line, perpendicular at a point on a line |