Activity 12.1
Equipment: You will need a compass, pair of scissors, ruler and protractor for this
activity.
Purpose: To discover a formula for
the area of a circle.
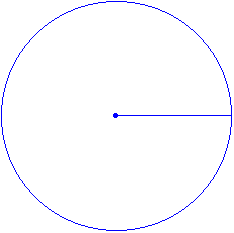
Step 1: Using the compass, draw a circle of radius 7 cm.
Then mark the circle's centre and draw its radius.
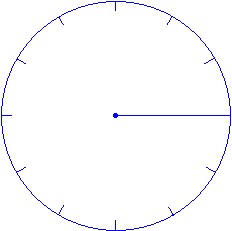
Step 2: Place the centre of the protractor at the centre of the
circle and the zero line along the radius. Then mark every 30º around the
circle.
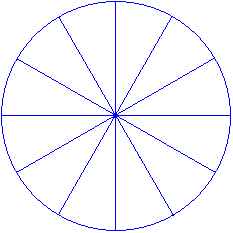
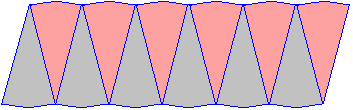
Step 3: Using a ruler and a pencil, draw lines joining each
30º mark to the centre of the circle to form 6 diameters. The diagram
thus obtained will have 12 parts as shown below.
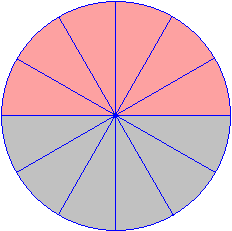
Step 4: Colour the parts as shown below.
Step 5: Cut out the circle and then cut along the diameters so
that all parts (i.e. sectors) are separated.
Step 6: Arrange all of the sectors to make a shape that
approximates a parallelogram as shown below.
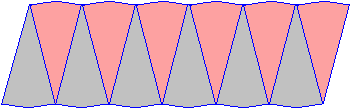
Step 7: Using a ruler, measure the base and the height of the
approximate parallelogram obtained in Step 6.
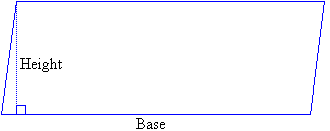
Questions:
1. Calculate the area of the figure in Step 6 by using the formula:
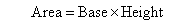
2. What is the area of the circle drawn in Step 1?
3. It appears that there is a formula for calculating the area of a
circle. Can you discover it?
Formula for the Area of a Circle

From the above activity, it is clear that by arranging the sectors of the
circle as a parallelogram that:
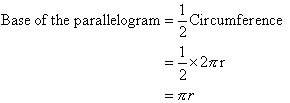
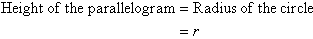
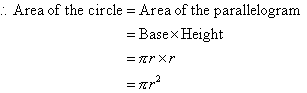
Remember:
The area, A, of a circle is given by the following formula where r is the radius of the circle:
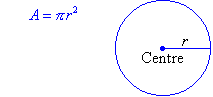
Example 8
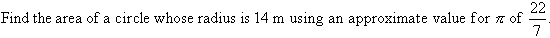
Solution:

So, the area is 616 m2.
Note:
To find the area of a region enclosed within a plane figure, draw a
diagram and write an appropriate formula. Then substitute the given values
and use a calculator, if necessary, to obtain the required area.
Example 9
Find the area of a circle of whose diameter is 11 cm using π = 3.14. Round your answer to 2 decimal places.
Solution:
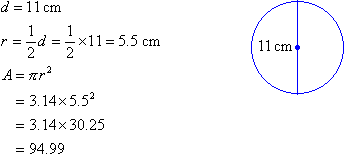
So, the area is 94.99 cm2.
|