| If the plotted points make a pattern, then the coordinates of each point may
have the same relationship between the x and y values.
In such a case, the x and y values are connected by a certain
rule.
A linear pattern is said to exist when the points examined form a
straight line.
Example 2
a. Plot the points in the following table on a Cartesian
plane.
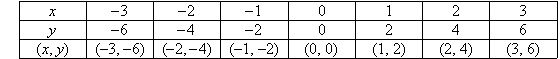
b. Describe the pattern in words.
c. State the next point in the pattern.
d. Find the rule that connects x and y.
Solution:
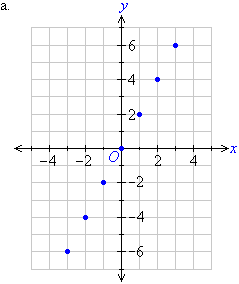
b. A linear pattern exists as the points form a straight
line. The pattern shows that as the x value increases by 1, the y value increases by 2.
c. The next x value will be 4 and the next y value
will be 8. So, the next point is (4, 8).
d. By trial and error, we look for a relationship between the
values of x and y.
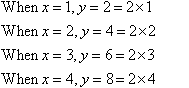
The above information for x and y indicates that the y-coordinate
is twice the x-coordinate. This means y is twice x.
So, the rule that connects the x-coordinate and the y-coordinate
is:
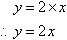
Example 3
a. Plot the following points on the Cartesian plane:
(–3, –9), (–2, –6), (–1, –3),
(0, 0), (1, 3), (2, 6), (3, 9)
b. Describe the pattern in words.
c. Find the rule that connects x and y.
Solution:
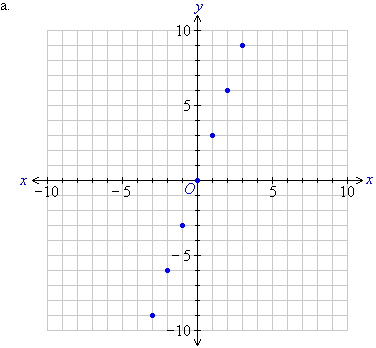
b. We notice that the points plotted on the Cartesian plane form a
straight line. So, a linear pattern exists. We can describe this
pattern in words as follows:
The y-coordinate is three times the x-coordinate.
This means y is three times x.
c. The rule that connects the x-coordinate and y-coordinate
is:
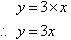
Example 4
a. Plot the following points on the Cartesian plane:
(–5, –7), (–4, –6), (–3, –5), (–2,
–4), (–1, –3), (0, –2), (1, –1), (2, 0), (3, 1),
(4, 2), (5, 3), (6, 4)
b. Describe the pattern in words.
c. Find the rule that connects x and y.
Solution:
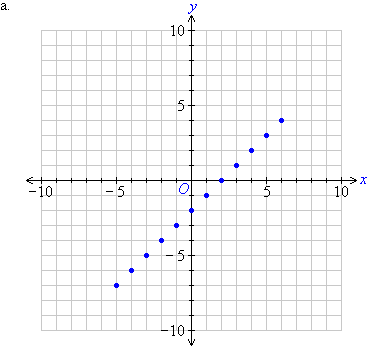
b. We notice that the points plotted on the Cartesian plane form a
straight line. So, a linear pattern exists. We can describe this
pattern in words as follows:
The y-coordinate is two less than the x-coordinate.
c. The rule that connects the x-coordinate and the y-coordinate
is:
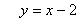
Key Terms
linear pattern |