| A sequence is a pattern of numbers that are formed in accordance with
a definite rule.
We can often describe number patterns in more than one way. To
illustrate this, consider the following sequence of numbers {1, 3, 5, 7, 9,
…}.
Clearly, the first term of this number pattern is 1; and the terms after
the first term are obtained by adding 2 to the previous term. We can
also describe this number pattern as a set of odd numbers.

By trial and error, we find that:
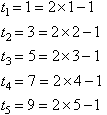
By observation, we notice that we can describe this number pattern by the
rule
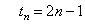
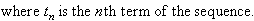
Formula and Tables
A table of values can be generated from the rule
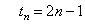
as shown below.
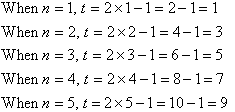

Finding the Algebraic Rule
We use algebra to study rules that describe the behaviour of everyday
things. For example, the behaviour of the height of a ball when it is
thrown upward or the amount outstanding for a loan after a number of regular
repayments. By finding a pattern in observed values (i.e.
measurements), we are often able to discover a rule that allows us to make
accurate predictions.
Using a Difference Pattern
When we try to discover an algebraic rule for ordered
pairs, we can find
the difference between two successive values of y. This allows
us to find a rule as illustrated below.
Consider the following table.
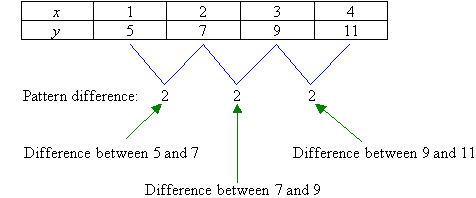
We notice that the values of x increase by just one at a time and
the difference between the successive values for y is 2. So, the rule
starts off with y = 2x. Will this give a correct answer from
the table? Let us check.
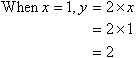
The answer is no. From the table, when x = 1 the
value of y should be 5. How do we change our answer from 2 to 5?
We
should add 3.
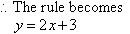
Check the rule to see if it is correct:
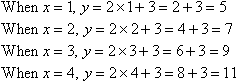
Example 5
Discover the rule for the following table of values:

Solution:
In the given table, the x-values increase by 1 for each ordered
pair.
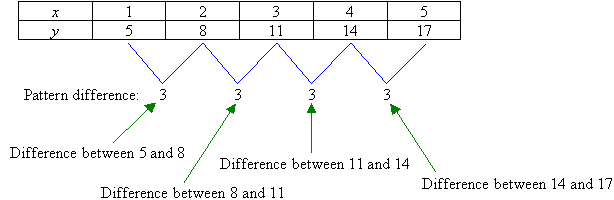
Find the difference between the successive values of y. That is:
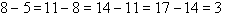
The difference between successive values of y is always 3. So, the
rule is of the form
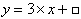
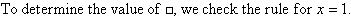
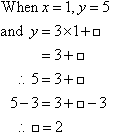
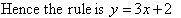
Check:
Check the rule to see if it is correct:
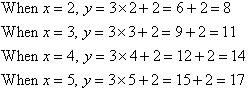
So, our rule is correct.
Note:
To establish a rule for a number pattern involving ordered
pairs of x and y, we can
find the difference between every two successive values of y. If the
difference pattern is the same, then the coefficient of x in the algebraic rule (or formula) is the same as the difference pattern.
Key Terms
number pattern, sequence, algebraic
rule, difference pattern |