| To solve the simultaneous
equations, make the coefficients of one of the
variables the same value in both equations. Then either add the equations
or subtract one equation from the other (whichever is appropriate) to form
a new equation that only contains one variable. This is referred to as eliminating the variable.
Solve the equation thus obtained. Then substitute the value found for
the variable in one of the given equations and solve it for the other
variable. Write the solution as an ordered pair.
Example 4
Solve the following simultaneous equations by using the elimination
method:
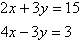
Solution:
Label the equations as follows:
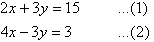
Notice that 3y appears on the left-hand side of both
equations. Adding the left-hand side of (1) and (2), and then the
right-hand sides, gives:
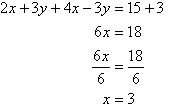
Note:
We have added equals to equals, and addition eliminates y.
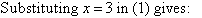
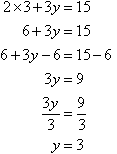

Example 5
Solve the following simultaneous equations by using the elimination
method:
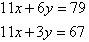
Solution:
Label the equations as follows:
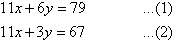
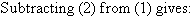
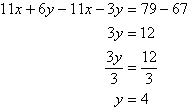
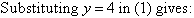
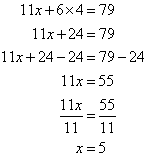
So, the solution is (5, 4)
Example 6
Solve the following simultaneous equations by using the elimination
method:
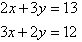
Solution:
Label the equations as follows:
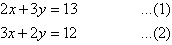
Multiplying (1) by 2 and (2) by 3 gives:
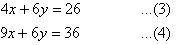
Subtracting (3) from (4) gives:
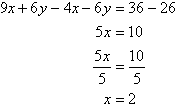
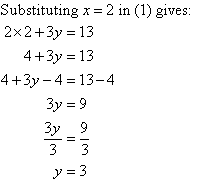
So, the solution is (2, 3).
Equations Containing Fractions
If either or both equations contain fractions, then it is desirable to
remove the denominators before solving them simultaneously.
Example 7
Solve the following simultaneous equations by using the elimination
method:
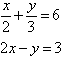
Solution:
Label the equations as follows:
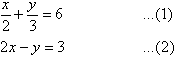
To simplify equation (1), multiply both sides by 6, the lowest common
denominator of 2 and 3.
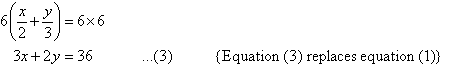
The equations are now:
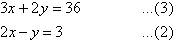
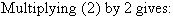

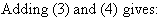
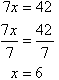
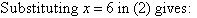
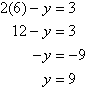
So, the solution is (6, 9).
Key Terms
elimination method, ordered pair |