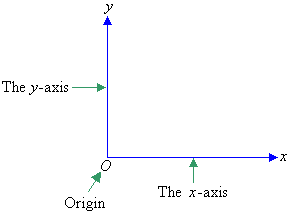
| The position of a point on a Cartesian plane is represented by
referring to it in terms of a horizontal line and a vertical line,
which are called the x-axis and y-axis respectively. The point of intersection of the x-axis and the y-axis
is called the origin.
Often, we draw a set of axes on graph paper as shown below.
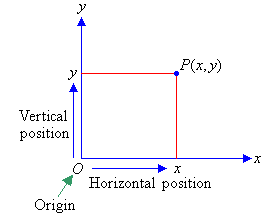
The position of any point on the Cartesian plane is described by using
two numbers, (x, y), that are called coordinates. The first number, x,
is the horizontal position of the point from the origin. It is called
the x-coordinate. The second number, y, is the vertical
position of the point from the origin. It is called the y-coordinate.
Since a specific order is used to represent the coordinates, they are
called ordered pairs.
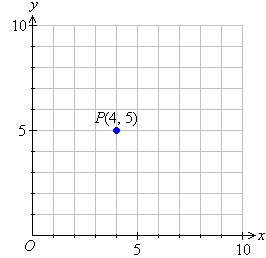
For example, an ordered pair (4, 5) represents a point 4 units to the
right of the origin in the direction
of the x-axis, and 5 units above the origin in the direction of the y-axis as
shown in the diagram below.
We say that:
The x-coordinate of point P is 4; and the y-coordinate
of point P is 5.
Or simply, we can say that:
The coordinates of point P are (4, 5).
Note the following:
- For the point P(4, 5), the ordered pair is (4, 5). So:
4 is the x-coordinate, and
5 is the y-coordinate.
- P(4, 5) means P is 4 units to the right of and 5 units
above the origin.
Example 3
State the coordinates of each of the points shown on the Cartesian plane:
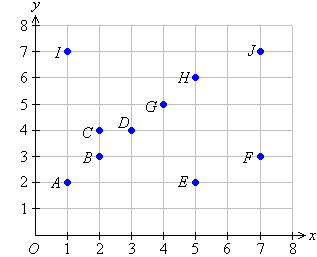
Solution:
A is 1 unit to the right of and 2 units above the origin. So, point A is (1, 2).
B is 2 units to the right of and 3 units above the origin. So, point B is (2, 3).
C is 2 units to the right of and 4 units above the origin. So, point C is (2, 4).
D is 3 units to the right of and 4 units above the origin. So, point D is (3, 4).
E is 5 units to the right of and 2 units above the origin. So, point E is (5, 2).
F is 7 units to the right of and 3 units above the origin. So, point F is (7, 3).
G is 4 units to the right of and 5 units above the origin. So, point G is (4, 5).
H is 5 units to the right of and 6 units above the origin. So, point H is (5, 6).
I is 1 unit to the right of and 7 units above the origin. So, point I is (1, 7).
J is 7 units to the right of and 7 units above the origin. So, point J is (7, 7).
Key Terms
point, Cartesian plane, horizontal line, x-axis, vertical line, y-axis, origin, axes, x-coordinate, y-coordinate, coordinates, ordered pairs, vertical
position, horizontal position |