Recall:
The four basic mathematical operations are:

Addition
Adding two (or more) numbers means to find their sum (or
total). The symbol used for addition is '+'.
For example, 5 + 10 = 15
This is read as five plus ten is equal to fifteen or simply, five plus
ten is fifteen.
Example 1
Find the sum of 9 and 8.
Solution:
9 + 8 = 17
Addition of Large Numbers
To add large numbers, list them in columns and then add only those digits
that have the same place value.
Example 2
Find the sum of 5897, 78, 726 and 8569.
Solution:
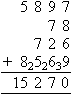
Note:
- Write the numbers in columns with the thousands, hundreds, tens and units
lined up.
- 7 + 8 + 6 + 9 = 30. Thus, the sum of the digits in the units column is 30. So, we place 0
in the units place and carry 3 to the tens place.
- The sum of the digits in the tens column after adding 3 is 27.
So, we place 7 in the tens place and carry 2 to the hundreds place.
- The sum of the digits in the hundreds column after adding 2 is
22. So, we place 2 in the hundreds place and carry 2 to the
thousdands place.
Subtraction
Subtracting one number from another number is to find the difference
between them. The symbol used for subtraction is '–'. This is
known as the minus sign.
For example, 17 – 8 = 9
This is read as seventeen take away eight is equal to nine (or seventeen
take away eight is nine). Also, we can say that 17 minus 8 is 9.
Example 3
Subtract 9 from 16.
Solution:
16 – 9 = 7
Subtraction of Large Numbers
To subtract large numbers, list them in columns and then subtract only
those digits that have the same place value.
Example 4
Find the difference between 7064 and 489.
Solution:

Note:
- Use the equals addition method or the decomposition method.
- Line up the thousands, hundreds, tens and units place values for the
two numbers when placing the smaller number below the larger number as
shown above.
Multiplication
Multiplication means times (or repeated addition). The symbol
used for multiplication is '×'.
For example, 7 × 2 = 14
This is read as seven times two is equal to fourteen or simply, seven times
two is fourteen.
To multiply a large number with another number, we write the numbers
vertically and generally multiply the larger number with the smaller number.
Note:
A product is the result of the multiplication of two (or more)
numbers.
Example 5
Calculate 765 × 9.
Solution:
Write the smaller number, 9, under the larger number, 765, and then
calculate the multiplication.
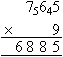
Note:
- 9 × 5 = 45. So, place 5 units in the units column and carry the
4 (i.e. four tens) to the tens column.
- Calculate 9 × 6 and then add 4 to give 58 (i.e. 58 tens). Then
place 8 in the tens column and carry 5 to the hundreds column.
- Finally multiply 7 by 9 and add 5 to give 68 (i.e. 68 hundreds).
Write this number down as shown above.
Remember:
- To multiply two large numbers, write the numbers vertically with the
larger number generally being multiplied by the smaller number which is called the
multiplier.
- We use the 'times table' to find the product of the larger number with
each digit in the multiplier, adding the results.
- Remember to add a zero for every place value after the multiplying
digit. For example, if the multiplying digit is in the
hundreds column, add two zeros for the tens column and for the units
column.
Example 6
Calculate 38 × 70.
Solution:
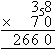
Note:
- Multiplying 38 by 70 is quicker than multiplying 70 by 38 as 70
contains a zero.
- A zero is placed in the units column. Then we calculate 7 × 38
as shown above.
Example 7
Calculate 385 × 500.
Solution:
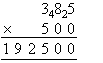
Note:
- Multiplying 385 by 500 is quicker than multiplying 500 by 385 as 500
contains two zeros.
- A zero is placed in the units column and also the tens column.
Then we calculate 5 × 385 as shown above.
Example 8
Calculate 169 × 68.
Solution:
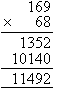
Note:
- To multiply 169 by 68, place 68 below 169.
- Then we calculate 8 × 169 and 60 × 169 as shown above.
Division
Division 'undoes' multiplication and involves a number called the dividend being 'divided' by another number called the divisor. The
symbol used for division is '÷'.
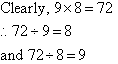
Example 9
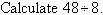
Solution:

Example 10
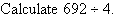
Solution:
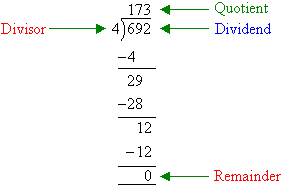
Note:
- As division is the inverse of multiplication, start by dividing 4 into
the column furthest to the left.
- 6 ÷ 4 = 1 and 2 is the remainder.
- Clearly, the remainder 2 is 200 (i.e. 20 tens); and we can carry this
into the tens column to make 29.
- Now, 29 ÷ 4 = 7 with a remainder of 1. Clearly, the remainder
of 1 is 10 (i.e. 10 units) and we carry this into the units column to
make 12.
- Finally, 12 ÷ 4 = 3.
Example 11
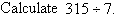
Solution:
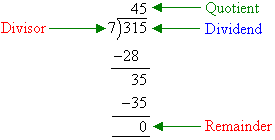
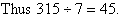
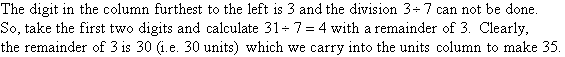
Summary
- The four basic mathematical operations are:

- Adding two (or more) numbers means to find their sum (or total).
- Subtracting one number from another number is to find the difference
between them.
- Multiplication means times (or repeated addition). A product is
the result of the multiplication of two (or more) numbers.
- Division 'undoes' multiplication.
Key Terms
basic operations, addition, sum, total, subtraction, difference, minus sign, equals
addition method, decomposition method, multiplication, times, repeated addition, product, division, dividend, divisor, quotient, remainder |