| A map cannot be of the same size as the area it represents. So, the
measurements are scaled down to make the map of a size that can be
conveniently used by users such as motorists, cyclists and
bushwalkers. A scale drawing of a building (or bridge) has the same
shape as the real building (or bridge) that it represents but a different
size. Builders use scaled drawings to make buildings and bridges.
A ratio is used in scale drawings of maps and buildings. That is:

Likewise, we have:

A scale is usually expressed in one of two ways:
- using units as in 1 cm to 1 km
- without explicitly mentioning units as in 1 : 100 000.
Note:
A scale of 1 : 100 000 means that the real distance is 100 000 times the
length of 1 unit on the map or drawing.
Example 14
Write the scale 1 cm to 1 m in ratio form.
Solution:
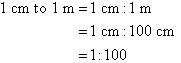
Example 15
Simplify the scale 5 mm : 1 m.
Solution:
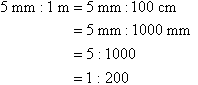
Example 16
Simplify the scale 5 cm : 2 km.
Solution:
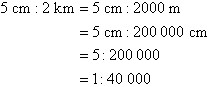
Calculating the Actual Distance using the Scale
If the scale is 1 : x, then multiply the map distance by x to calculate the actual distance.
Example 17
A particular map shows a scale of 1 : 5000. What is the actual
distance if the map distance is 8 cm?
Solution:
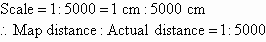
Map distance = 8 cm
Let the actual distance be a cm.

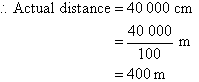
Alternative Way:
Map distance = 8 cm
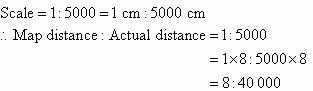
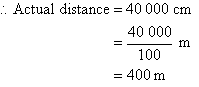
Calculating the Scaled Distance using the Actual Distance
If the scale is 1 : x, then divide the actual distance by x to calculate the map distance.
Example 18
A particular map shows a scale of 1 cm : 5 km. What would the map
distance (in cm) be if the actual distance is 14 km?
Solution:

So, the map distance is 2.8 cm.
Alternative Way:

So, the map distance is 2.8 cm.
Key Terms
scale drawing, map, scaled
down, scale of a drawing, map
scale |