Year 7 Interactive Maths - Second Edition

Multiplication

For example, 4 × 6 = 24.

This is read as four times six is equal to twenty-four or simply, four times six is twenty-four.

Note:

Knowledge of multiplication is very important.  So, if you are weak in multiplication, you must try to attain a proficiency in the following 'times table'.

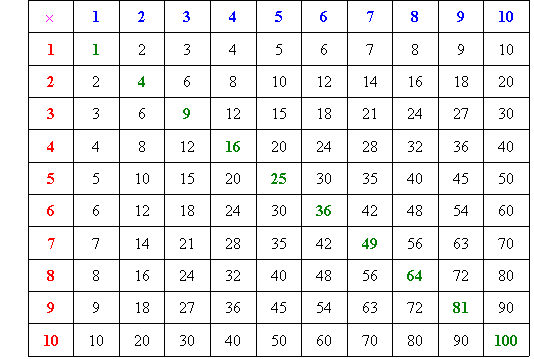
Your confidence and ability to learn mathematics will depend largely on your knowledge of multiplication.  So, you should aim to master the above 'times table'.

Example 8

Find the product of 8 × 9.

Solution:

8 × 9 = 72

Note:

• A product is the result of multiplication of two (or more) numbers.
• To calculate 8 × 9, we recall the 'eight times table'.

Multiplication of Large Numbers

To multiply a large number with another number, we may use short multiplication or long multiplication.

Short Multiplication

• To multiply a large number by a single digit number, write the numbers vertically with the larger number being multiplied by the smaller number.
• We then use the 'times table' to find the product of the numbers as illustrated in the following example.

Example 9

Calculate 89 × 7.

Solution:

To calculate 89 × 7, set it out vertically with the smaller number placed under the larger number as shown below. Then calculate 7 × 9.

Now, calculate 7 × 8 and add 6 to obtain 62. This is written as shown below.

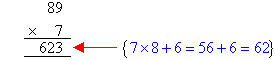
Setting Out

We often set out the solution as follows:

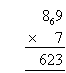
Note:

• 7 × 9 = 63.  So place 3 in the units column and carry the 6 (i.e. six tens).
• Then calculate 7 × 8 and add 6 to obtain 62 (i.e. 62 tens).

Example 10

Calculate 38 × 60.

Solution:

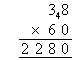
Note:

• Multiplying 38 by 60 is quicker than multiplying 60 by 38 as 60 contains a zero.
• A zero is placed in the units column. Then we calculate 6 × 38 as shown above.

Example 11

Calculate 385 × 500.

Solution:

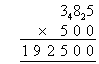
Note:

• Multiplying 385 by 500 is quicker than multiplying 500 by 385 as 500 contains two zeros.
• A zero is placed in the units column and also the tens column.  Then we calculate 5 × 385 as shown above.

Long Multiplication

• To multiply two large numbers, write the numbers vertically with the larger number being multiplied by the smaller number which is called the multiplier.
• We use the 'times table' to find the product of the larger number with each digit in the multiplier, adding the results.
• Remember to add a zero for every place value after the multiplying digit.  For example, if the multiplying digit is in the hundreds column, add two zeros for the tens column and for the units column.

Example 12

Calculate 269 × 78.

Solution:

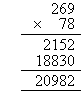
Note:

• To multiply 269 by 78, place 78 below 269.
• Then we calculate 8 × 269 and 70 × 269 as shown above.

Commutative Law for Multiplication

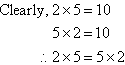
In general:

If a and b are two numbers, then:

This is known as the Commutative Law for Multiplication.

Associative Law for Multiplication

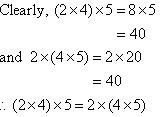
In general:

If a, b and c are three numbers, then:

This is known as the Associative Law for Multiplication.

Example 13

Calculate 3 × 2 × 5.

Solution:

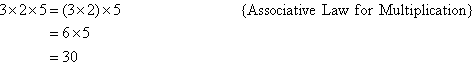
Example 14

Calculate 7 × 5 × 4.

Solution:

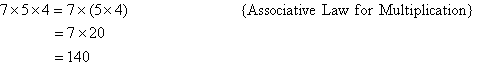
Key Terms

multiplication, times, times table, product, short multiplication, long multiplication, Commutative Law for Multiplication, Associative Law for Multiplication