| A plane is a flat or level surface in two dimensions. Figures
such as circles or squares have all of their parts lying on a plane and
thus, are examples of plane figures.

A triangle is a closed plane figure bounded by three line segments.
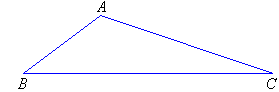

Types of Triangles
Triangles can be classified according to the length of their sides and
the size of their angles.
Classifying Triangles according to the Length of their Sides
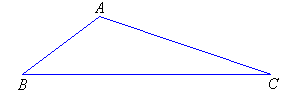
Scalene Triangles
A scalene triangle has no equal sides.
Equilateral Triangles
An equilateral triangle has all sides equal.
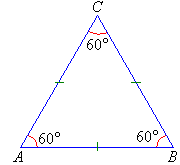
All angles of an equilateral triangle are 60°.
Note:
- To show that the sides of an equilateral triangle have the same length,
we place identical marks on the sides of the triangle.
- To show that the angles of an equilateral triangle are equal in size,
we place identical curves on each angle.
Isosceles Triangles
An isosceles triangle has two sides equal.
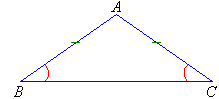
The angles opposite the equal sides are equal.
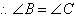
Note:
- In the diagram, side BC has a different length to AB and AC.
- The side of the isosceles triangle that has a different length is said
to be the base of the triangle. So, BC is the base.
- Identical marks on the sides indicate that the sides are equal.
- Identical marks on the angles indicate that the angles are equal.
Example 1
Classify each of the following triangles according to the lengths of
their sides:
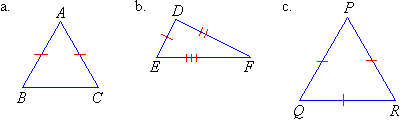
Solution:
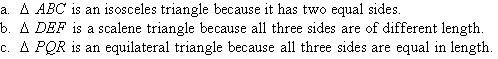
Classifying Triangles according to the Size of their Angles
Acute-angled Triangles
An acute-angled triangle has all angles less than 90º (i.e. all
three angles are acute).
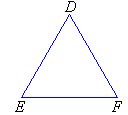
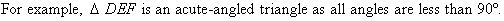
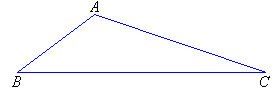
Obtuse-angled Triangles
An obtuse-angled triangle has one angle greater than 90º. That
is, one angle is obtuse.
Right-angled Triangles
A right-angled triangle has one angle equal to 90°. That is,
one angle is a right angle.
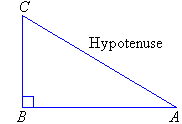
Note:
- The side opposite the right angle is called the hypotenuse.
- The hypotenuse is the longest side of the triangle
(which can be verified with a ruler).
Example 2
Classify each of the following triangles according to the size of their
angles
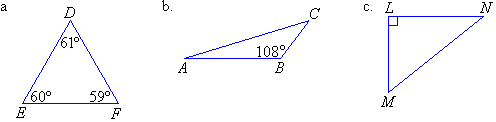
Solution:
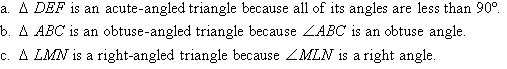
Activity 1

Key Terms
plane, plane figure, triangle, scalene triangle, equilateral
triangle, isosceles triangle, acute-angled
triangle, obtuse-angled triangle, right-angled
triangle, hypotenuse |